Information source set modelling: a very simple and brief introduction.

My objective in this post to very briefly present an outline of a diagramming and modelling convention for sets of interacting (causally, or channel connected) information sources.

In my forthcoming monograph, I present a theory of natural and artefactual information types. This theory is accompanied by a modelling language and modelling technique. It is adapted, with almost no changes apart from the semantics (which are similar), from a comparatively old, and very simple, diagrammatic modelling technique familiar to data scientists from the 1960s: data flow modelling using the data flow diagram (DFD). I use a close adaptation of this diagram and its conventions to model information flow in networks of interconnected information sources. The technique bears some similarity to the modelling of neural network hidden layers, familiar especially from the work of cognitive neuroscientist Karl Friston (Kirchhoff et al., 2018). However, DFDs are not Bayesian nets, and Bayesian inference is not part of their semantics. Nor is the Bayesian component important to source set modelling (although there is no reason in principle why it cannot be incorporated along with Markov Blankets).

The approach does not have the unidirectal throughput from input to cost function familiar in neural nets, nor the uniform layers or ranks of nodes. It is essentially a directed acyclic graph with unidirectional flow relations. Here are the elements of the language.

(DFDs are essentially directed acyclic graphs (DAGs) with other semantical elements added for the purpose of modelling data flow.)

Information source set and flow diagramming elements:

Figure 1

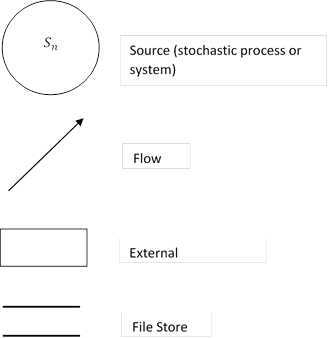
The following are some examples of the use of the modelling convention as applied to different source sets and source inter-transmission dynamics.

Ghost Channel

Here is a representation of the ghost (or virtual) channel of Fred Dretske:

Figure 2

Virtual Source

Figure 3

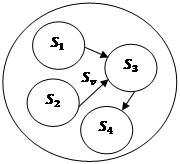
Note: Channels included in a virtual source might be virtual or ghost channels

Pseudo Source

Figure 4

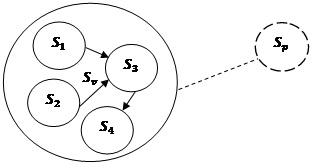
In the next post I will briefly outline the theory of natural information types that accompanies this diagramming and modelling system.

References

Dretske, F. (1981). Knowledge and the flow of information. Blackwell.

Friston, K. J., Trujillo-Barreto, N., & Daunizeau, J. (2008). DEM: A variational treatment of dynamic systems. NeuroImage, 41(3), 849–885. https://doi.org/10.1016/j.neuroimage.2008.02.054